Karnaugh Map

The Karnaugh Map (K-map for short) is a method to simplify Boolean Algebra expressions.
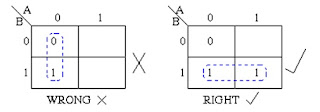
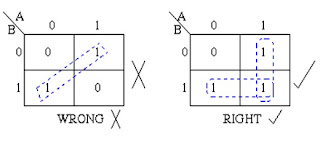
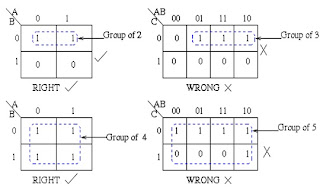
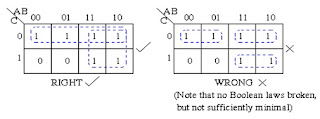
The Karnaugh Map reduces the need for extensive calculations by taking advantage of human's pattern-recognition capability.
It also permits the rapid identification and elimination of potential race conditions.


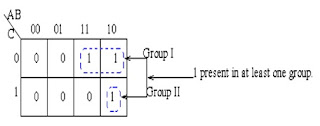
Here's an example of the Karnaugh Map.

The Karnaugh Map also provides a pictorial method of grouping together expressions with common factors and therefore eliminating unwanted variables.
The Karnaugh Map can also be described as a special arrangement of a Truth Table.


The diagram below shows the correspondence between the Karnaugh Map and the Truth Table for the general case of a two variable problem.



The values inside the squares are copied from the output column of the Truth Table , therefore there is one square in the map for every row in the Truth Table.
Around the edge of the Karnaugh Map are the values of the two input variable.
A is along the top and B is down the left hand side.
The diagram below explains this :


The values around the edge of the map can be thought of as coordinates. So an example , the square on the top right hand corner of the map in the above diagram has coordinates A=1 and B=0. This square corresponds to the row in the truth table where A=1 , B=0 and F=1.

Rules of simplification

Groups may not include any cell containing a zero .

Groups may be horizontal or vertical, but not diagonal. 

Groups must contain 1, 2, 4, 8, or in general 2n cells. 

That is if n = 1, a group will contain two 1's since 21 = 2. 

If n = 2, a group will contain four 1's since 22 = 4. 

Each group should be as large as possible.

Each cell containing a one must be in at least one group. 

Multiplication & Division

So previously you've learnt about Addition and Subtraction from my fellow mate's post Addition & Subtraction.

Now you will learn more about Multiplication and Division.

Multiplication

Compared with addition and subtraction, multiplication is much more complex operation in both hardware and software.
A wide variety of algorithms have been used in various computers. We start off with the binary multiplication.

Rules of Multiplication

0 x 0 = 0

0 x 1 = 0

1 x 0 = 0

1 x 1 = 1

Example :

   101

x   11

   101  < Firstly , Multiply 101(Multiplicand) to 1(Multiplier) like the ordinary multiplication.

 1010  < Then , add 0 as a placeholder as we would in decimal multiplication , and multiply 101 with 1.

 1111  < Lastly , add 101 (Product of the first multiplication) and 1010 (Product of the second multiplication)

Another example for Binary Multiplication :

          1011  Multiplicand (11)

    x    1101  Multiplier (13)

          1011

        0000    Partial Products

      1011

    1011      

   10001111 Product (143)

#Note : Length of product is the sum of operand lengths.

Flowchart for Unsigned Binary Multiplication

                                            Division

Division is somewhat more complex than multiplication but is based on the same general principles. As before , the operation involves repetitive shifting and addition or subtraction.

Here's an example of binary division :

        11  R = 10

11 ) 1011

      -11

         101

       -11

           10  <  Remainder , R

Flowchart for Unsigned Binary Division

CHAPTER 2:

Floating Point

6 to represent real numbers on computers.

6 reals in scientific notation which represents numbers as a base number and an exponent. The base for the scaling is normally 2, 10 or 16.

} Scientific notation

◦     ±___.___ x 10^__

◦     –2.34      × 10⁵⁶       (normalized)

◦     +0.002    × 10^–4     (not normalized)

◦     +987.02  × 10⁹     (not normalized)

} Scientific notation in binary

◦     ±1.______₂ × 2^___

  Example:

1.0101₂    x  2⁴

-1.10011₂ x  2¹²

1.0001₂     x  2^-3

A. Floating Point Standard

} Defined by IEEE Std 754

} Developed in response to divergence of representations

◦     Portability issues for scientific code

} Two representations

◦     Single precision (32-bit)

◦     Double precision (64-bit)

B. IEEE Floating-Point Format

Bit	s	Exponent	Fraction
single(32)	1	8	23
double(64)	1	11	52

} x = (-1)^s x (1 + Fraction ) x 2^{(Exponent-Bias)}

}S: sign bit (0 Þ positive, 1 Þ negative)

} Normalize significand:

1.0 ≤ |significand| < 2.0

} Exponent: excess representation: actual exponent + Bias

◦     Ensures exponent is unsigned

◦     Single: Bias = 127; Double: Bias = 1203

C. Floating-Point Example

} Represent is –45.75

1^st: change 45.75 to binary form

         (a)                               (b)

45=32+8+4+1              45/2 = 22 r 1

=2⁵+2³+2²+2⁰         22/2 = 11 r 0

=101101₂                 11/2 = 5 r   1 

                              5/2 = 2 r   1  

                              2/2 = 1 r   0   

                              1/2 = 0 r   1  ↑

 45 = 101101₂

            (a)                              (b)

0.75 = 0.5 + 025      0.75 x 2 = 1.5  1 ↓

= 2^-1 + 2^-2        0.5 x 2 = 1.0   1

= 0.11₂             

        0.75 = 0.11₂

45.75 = 101101₂ + 0.11₂

= 101101.11₂

2^nd: change the –45.75 to formula below

 x = (-1)^s x (1 + Fraction ) x 2^{(Exponent-Bias)}

–45.75 = –1 x (101101.11₂)

      = –1 x 1.0110111₂ x 2⁵

      = –1¹ x (1 + 0.0110111₂) x 2⁵

(the exponent is 5 because the decimal are move to the left hand side with 5 digit places.)

3^rd: list out the information

S = 1                          ( negative )

Fraction = 0110111……00₂

Exponent = 5+ Bias   ( Bias of single = 127)

                         = 5 + 127  

                         = 132

= 10000100₂

(the exponent must in the base 2)

s	Exponent	Fraction
1	10000100	0110111……00

※ Single: 1100001000110111……00

D. Floating-Point Example

} What number is represented by the single-precision float

               010000011011100……00

 1^st: list out the information

S = 0

Fraction = 01110…00₂

Exponent = 10000011₂

        = 2⁷ + 2¹ + 2⁰

        = 131

2^nd: replace the information into the equation

}x = (-1)^s x (1 + Fraction ) x 2^{(Exponent-Bias)}

} x = (–1)⁰× (1 + 0.0111₂) × 2^{(131 – 127)}

           = (1) × 1.4375 x 2⁴

※         =  23

the end ^^

if you have any questions or ideas can contact me 

Prepared    By      :    TEE SONG WEI

Contact Number :       0173403160 

Facebook : Wentson Tee Song Wei

Logic Gate

Definition of Logic Gate

•  A logic gate is an idealized or physical device implementing a Boolean function. Logic gates perform basic logical functions and are the are the fundamental building blocks of digital integrated circuits. Most logic gates take an input of two binary values, and output a single value of a 1 or 0. Some circuits may have only a few logic gates, while others, such as microprocessors, may have millions of them. There are seven different types of logic gates, which are outlined below. 

•  In the following examples, each logic gate except the NOT gate has two inputs, A and B, which can either be 1 (True) or 0 (False). The resulting output is a single value of 1 if the result is true, or 0 if the result is false.

1.  AND - True if A and B are both True

2.  OR - True if either A or B are True

3.  NOT - Inverts value: True if input is False; False if input is True

4.  XOR - True if either A or B are True, but False if both are True

5.  NAND - AND followed by NOT: False only if A and B are both True

6.  NOR - OR followed by NOT: True only if A and B are both False

7.  XNOR - XOR followed by NOT: True if A and B are both True or both False

THE AND GATE
ØAn AND gate is a logic circuit that performs the AND

   operation on the circuit’s inputs.
Ø The AND gate operation is performed by multiplication of 1s and 0s.
ØThe Boolean expression for AND operation is :

                Output = A . B
Ø If 0  is called “false” and 1 is called “true”, an output of
   AND gate will only get 1 if both input of AND gate is 1.
   Otherwise, the output will be always 0 .

AND gate

Input A	Input B	Output
	1
1
1	1	1

THE OR GATE
ØAn OR gate is a logic circuit that performs an OR operation on the circuit’s input.
Ø  The output is "true" if either or both of the inputs are "true." If both inputs are "false," then the output is "false."
Ø  The Boolean expression for OR operation is :
                              Output = A + B

         

                           OR gate

Input A	Input B	Output
	1	1
1		1
1	1	1

THE NOT GATE

Ø A logical inverter , sometimes called a NOT gate to differentiate it from other types of electronic inverter devices, has only one input. It reverses the logic state.

                                         

THE NAND GATE
ØThe NAND gate is a combination of NOT - AND.

ØIt acts in the manner of the logical operation " and " followed by a negation. The output is "false" if both inputs are "true".
    Otherwise the outputs is "true"

ØThe Boolean expression of NAND  operation is :
                                    Output = A' . B'

                                                 NAND gate

Input A	Input B	Output
		1
	1	1
1		1
1	1

THE NOR GATE
ØThe NOR gate is a combination OR gate followed by an inverter. Its outputs is "true" if both inputs are "false". Otherwise , the outputs is "false"

ØThe Boolean expression of NOR operation is :
                                Output = A' + B'

NOR gate

Input A	Input B	Output
		1
	1
1
1	1

THE EXCLUSIVE-OR / XOR GATE

ØThe Boolean expression of XOR operation is :

                               Output = A . B' + A' . B

                                         XOR gate

Input 1	Input 2	Output
	1	1
1		1
1	1

THE EXCLUSIVE-NOR / XNOR GATE

ØThe XNOR (exclusive-NOR) gate is a combination XOR gate
   
    followed by an inverter. Its output is "true" if the inputs are the 
     
     same, and "false" if the inputs are different .

XNOR gate

Input A	Input B	Output
		1
	1
1
1	1	1

                               Written by EOH WENG JIAN (B031210151)